How to Know Which Error Propagation Formula to Use

Error SQRT. So the ME for the area of the coin goes from 346 to 491 square centimeters.

Propagation Of Uncertainty Rules For Estimating Uncertainty Isobudgets

The general formula for the propagation of errors is then 𝑅𝑅 2 2𝑅 2 2 where.

. However you can estimate the error in z sinx as being the difference between the largest possible value and the average value. In other words the absolute. The uncertainty should be calculated by using error propagation.

This is when you compare the size of your error to the size of the original quantity1 The formula for relative error is. For example because the area of a circle is proportional to the square of its diameter if you know the diameter with a relative precision of 5 percent you know the area with a relative precision of 10 percentFor example under certain assumptions the half-life t 12 of a drug in the body is related to the terminal elimination rate constant k e for the drug by the formula. Lets first look at the formula for adding or subtracting measurements with uncertainties.

The propagation of error formula for Y fX Z ldots a function of one or more variables with measurements X Z ldots gives the following estimate for the standard deviation of Y. P I2R u Let I 10 01 amp and R 10 1 W P 10 watts u calculate the variance in the power using propagation of errors P 10 2 watts n If the true value of the power was 10 W and we measured it many times with. For example length 191 004 m relative error 004191 002 or 2.

You use the first formula you gave when you have entirely uncorrelated errors where the standard variances the squares of the standard deviances add. If Q Qx is any function of x then the general formula for error propagation can be defined as. Measure Density of Earth.

Thus D sin x sinx D x - sinx. Using the absolute error Δx one adds the relative errors Δxx in quadrature. µ q xn xn 2 10501 8.

Note that youll rarely have to derive these formulas from scratch but it can be good to. How To Calculate Absolute Uncertainty This result is more commonly written by dividing both sides by f xy to give 3 Although the idea of error propagation may seem intimidating you have already been The precision of a set of measurements is a measure of the range of values found that is of the reproducibility of the measurements. The uncertainty in q is then q sµ q x1 x1 2.

If the result 𝑅 is a function of measurements where 𝑅. Here y is a measure of the absolute error whereas yy represents the relative error and yy 100 is the percent error. 21 or equivalently Q jQj jnj x jxj 22 The second form is probably easier to remember.

Independent and omit the covariance. And use similar techniques for other functions. Since I did a division in calculating the reduction I should use the formula.

There is an error propagation formula that is used for calculating uncertainties when adding or subtracting measurements with uncertainties and a different error propagation formula for calculating uncertainties when multiplying or dividing measurements with uncertainties. Gaussian distributions of errors are usually assumed. 2Actually you could change the modi er if you wanted to - for instance 12cm 1mm - but.

The fractional or percent uncertainty gets multiplied by jnjwhen you raise xto the nth power. The relative error of a product of two numbers is got by adding the relative errors of the numbers. Computations based on x eg.

If nis an exact number and Q xn then Q jnjxn 1 x. As a more concise rule of thumb. Error Propagation tutorialdoc Daley 2 10909 R i.

General Formula for Error Propagation Wemeasure x1x2xn withuncertainties x1x2xn. Each reading has an uncertainty of 002 mL according to the buret manufacturer. Often one refers to relative error as the percentage error.

There is usually some unknown error x associated with the measurement where the exact value is x x. RelX X jXj 1 Thus in the above example your 1cm uncertainty on your 589m measure-ment would turn into a relative error of 00016. The purpose of these measurements is to determine q which is a function of x1xn.

Calculate average density ρand determine which elements constitute the. The volume delivered by a 100-mL graduated cylinder is. General Formula for Error Propagation.

Propagation of Errors 3 u If x and y are correlated define sxy as. Qq q222 qx y z xy z. Power in an electric circuit.

δδ δ δ. Y fx will therefore have some error y fxx fx. The error propagation formula then reduces to Hdf L2 i k jj f ÅÅÅÅÅÅÅÅÅÅÅ x dx y zz 2 i k jj f ÅÅÅÅÅÅÅÅÅÅÅ y dy y zz 2 where we use the notation dx to represent an uncertainty instead of sx because we use an estimated uncertainty instead of an observed variance.

Using 21 for d in the area formula gives A 346 and using 25 for d gives A 491. Which should be equal to zero then you shouldnt use relative error. Main formula for error propagation always use this formula.

If your relative error is larger than 1 you should just use absolute error. So the error in the volume delivered. Called the propagated error.

Propagation Of Error Ib Physics Youtube

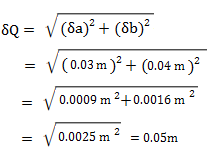
Error Propagation Propagation Of Uncertainty Statistics How To

Propagation Of Uncertainty Rules For Estimating Uncertainty Isobudgets